Terne di sequenza
I sistemi di generazione di potenza elettrica sono in massima parte sinusoidali e isofrequenziali. I sistemi distributivi di potenza elettrica sono in massima parte trifase e sono quindi descritti da terne di grandezze (tensioni, correnti, impedenze, ammettenze, ecc.).
È utile rappresentare ciascuna singola grandezza simbolicamente come un vettore rotante nel piano di Gauss facendo ricorso alla trasformata di Steinmetz: il fasore corrispondente contiene le informazioni di modulo e fase in un numero complesso.
Una terna di tensioni è simmetrica se ciascuna ha la stessa ampiezza ed è sfasata dalle altre di 120°, una terna di correnti è equilibrata se ciascuna ha la stessa ampiezza ed è sfasata dalle altre di 120°. Praticamente la stessa cosa, tuttavia l’aggettivo simmetrico è usato per le tensioni, l’aggettivo equilibrato si usa per le correnti, ne prendiamo atto.
La somma vettoriale di ogni terna simmetrica o equilibrata è nulla in ogni istante, cioè i tre vettori costituenti ciascuna terna costituiscono non solo una stella pura, ma anche un triangolo chiuso.
Fin qui il caso ideale, nella realtà i sistemi distributivi elettrici sono tutt’altro che simmetrici ed equilibrati non solo per la dissimmetria tra i componenti, ma soprattutto per l’inserzione dei carichi monofase che di fatto rendono spurie le terne di correnti e tensioni, di impedenze e ammettenze. Ne consegue una maggiore difficoltà di analisi, inoltre lo studio dei guasti, attività essenziale per garantire la qualità complessiva di esercizio delle reti elettriche, diventa ulteriormente oneroso per via dei transitori e di variabili aggiuntive necessarie per i calcoli.
Per questi aspetti viene in soccorso la teoria delle componenti simmetriche, sviluppata da Fortescue agli inizi del novecento, secondo cui qualunque terna di grandezze sinusoidali può essere rappresentata attraverso 3 terne di sequenza così descritte:
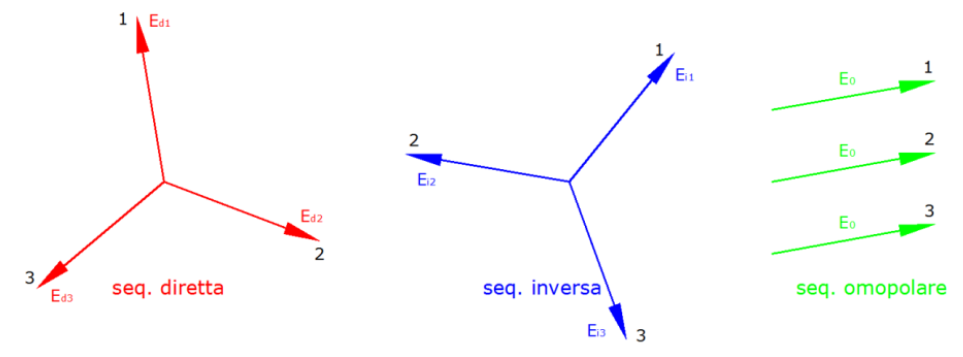
- terna di sequenza diretta (o sequenza positiva o dei ritardi) costituita da 3 fasori con lo stesso modulo e sfasati di 120°, rotanti in senso orario
- terna di sequenza inversa (o sequenza negativa o degli anticipi) costituita da 3 fasori con lo stesso modulo e sfasati di 120°, rotanti in senso antiorario
- terna di sequenza omopolare (o sequenza zero) costituita da 3 fasori con lo stesso modulo e a sfasamento nullo tra essi
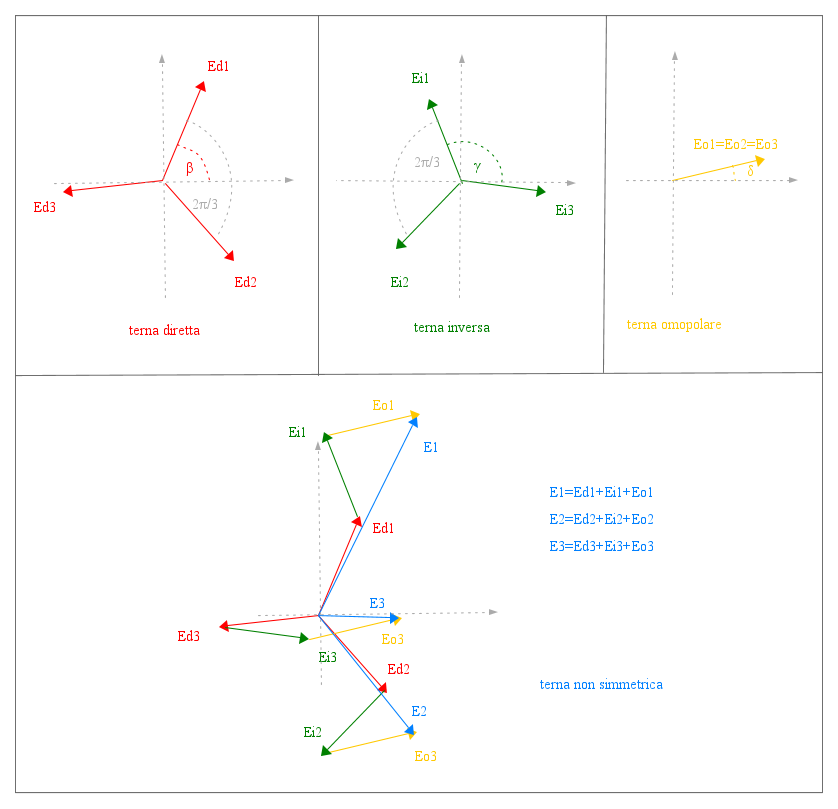
La somma delle 3 terne costituisce la terna originaria che si vuole analizzare. Le terne di sequenza diretta e inversa sono stelle pure, cioè sono composte ciascuna da 3 vettori di uguale modulo e sfasati di 120°, la terna di sequenza diretta ha la successione dei vettori 1-2-3 in senso orario, la terna di sequenza inversa ha la successione dei vettori 1-2-3 in senso antiorario, la terna di sequenza omopolare è costituita da 3 vettori identici in modulo e fase.
Le terne di sequenza si identificano attraverso il primo vettore, gli altri due si ricavano dalla rotazione di questo, nel caso dei vettori di sequenza diretta e inversa, oppure sono uguali a questo, nel caso dei vettori di sequenza omopolare.
| Il fulcro della trasformata di Fortescue è l’operatore di rotazione … |   |
| e le associate matrici di conversione diretta … |   |
| e inversa … |  |
Questa rappresentazione è applicabile a qualsiasi grandezza ed è utile in quanto riduce un problema complesso a una somma di problemi più semplici, si tratta di una trasformazione lineare cui è applicabile il principio di sovrapposizione degli effetti.
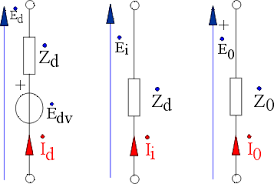
Risulta conveniente nell’analisi dei cortocircuiti nelle reti trifase in cui l’applicazione della trasformazione di Fortescue riduce la rete, vista dal punto di guasto, a un singolo generatore e impedenze di sequenza. In particolare il circuito di sequenza diretta è costituito da un generatore di tensione di valore Ed (tensione stellata del sistema considerato) con in serie l’impedenza Zd, il circuito di sequenza inversa è costituito dalla sola impedenza Zi, il circuito di sequenza omopolare è costituito dalla sola impedenza Zo.
Questa tecnica di analisi si adotta tipicamente per l’analisi dei guasti nelle reti dalla media tensione in su, tipicamente distribuite con tre fili senza il conduttore neutro.
Le reti trifase senza neutro possono essere affette dai seguenti guasti:
- Guasto monofase a terra
- Guasto bifase isolato
- Guasto bifase a terra
- Guasto trifase isolato
- Guasto trifase a terra
I cortocircuiti determinano, nelle sezioni di guasto, precisi vincoli che corrispondono ad altrettanti vincoli fra i relativi componenti sequenziali.
Collegando opportunamente tra loro i bipoli delle 3 sequenze si modellano i diversi tipi di guasto e si perviene alle reali correnti di c.to-c.to.
Si possono considerare riduzioni al metodo di calcolo e semplificazioni accettabili, anche legate al modo di esercizio del neutro delle reti di distribuzione considerate, che tipicamente sono i seguenti:
- Neutro isolato da terra
- Neutro collegato direttamente a terra
- Neutro collegato a terra tramite resistore
- Neutro collegato a terra tramite induttanza o neutro compensato (bobina di Petersen)




